Backpropagation 梯度推导 台湾国立大学应用深度学习
Backpropagation 算法推导
本文是NTU陈蕴侬教授,应用深度学习课程反向传播算法推导的笔记。原文在:200310_Backprop.pdf
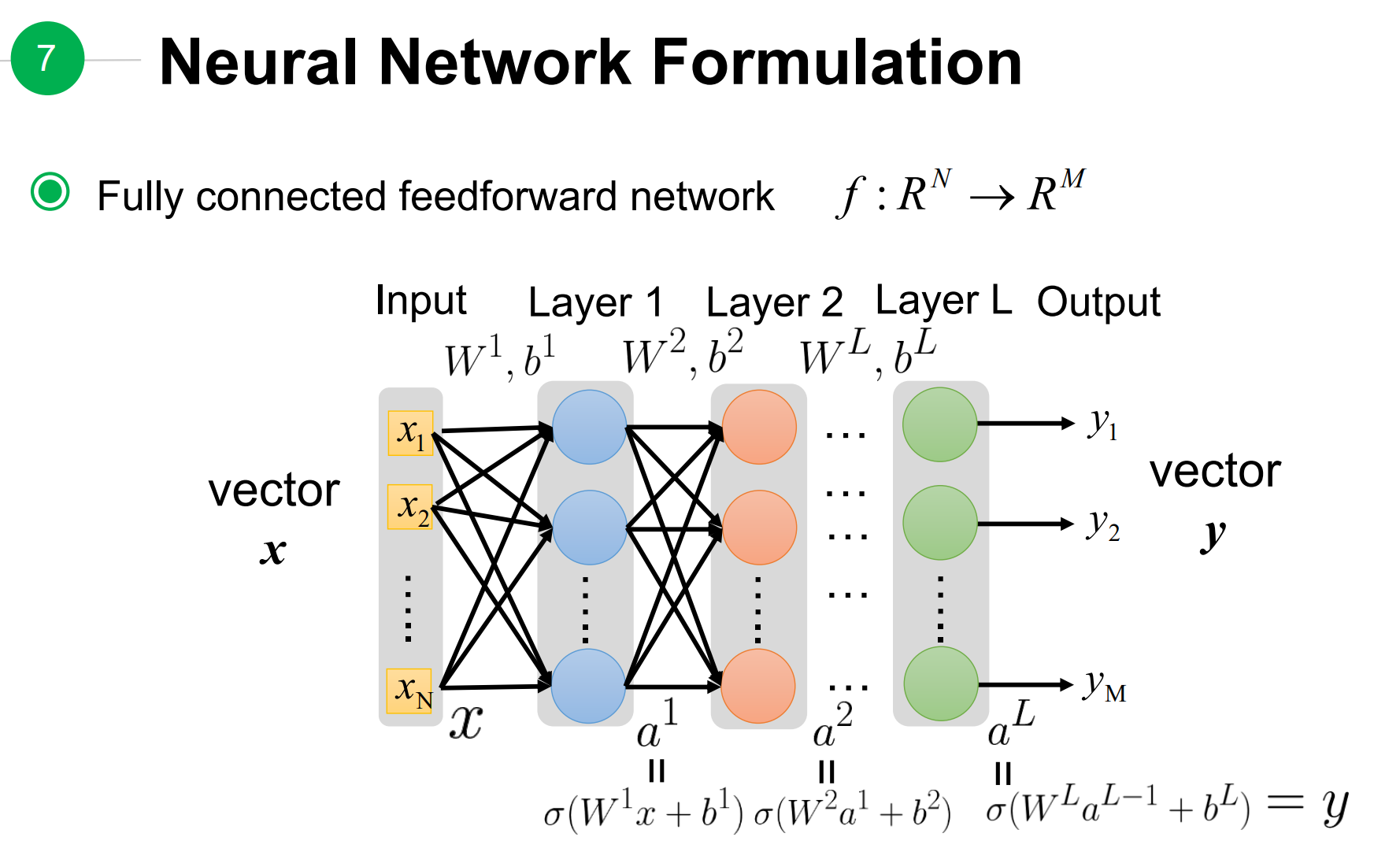
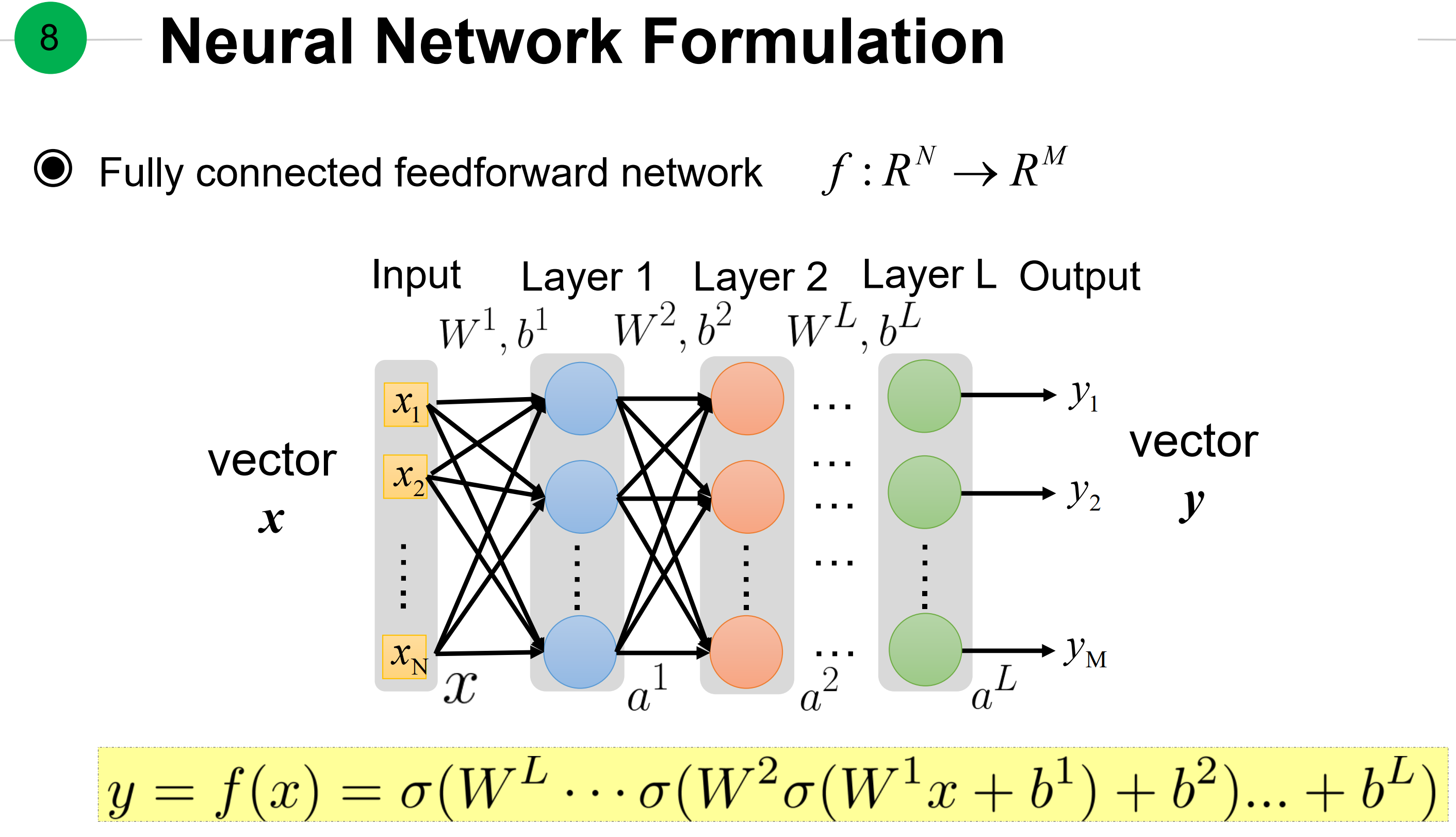
1. 全连接神经网络的公式
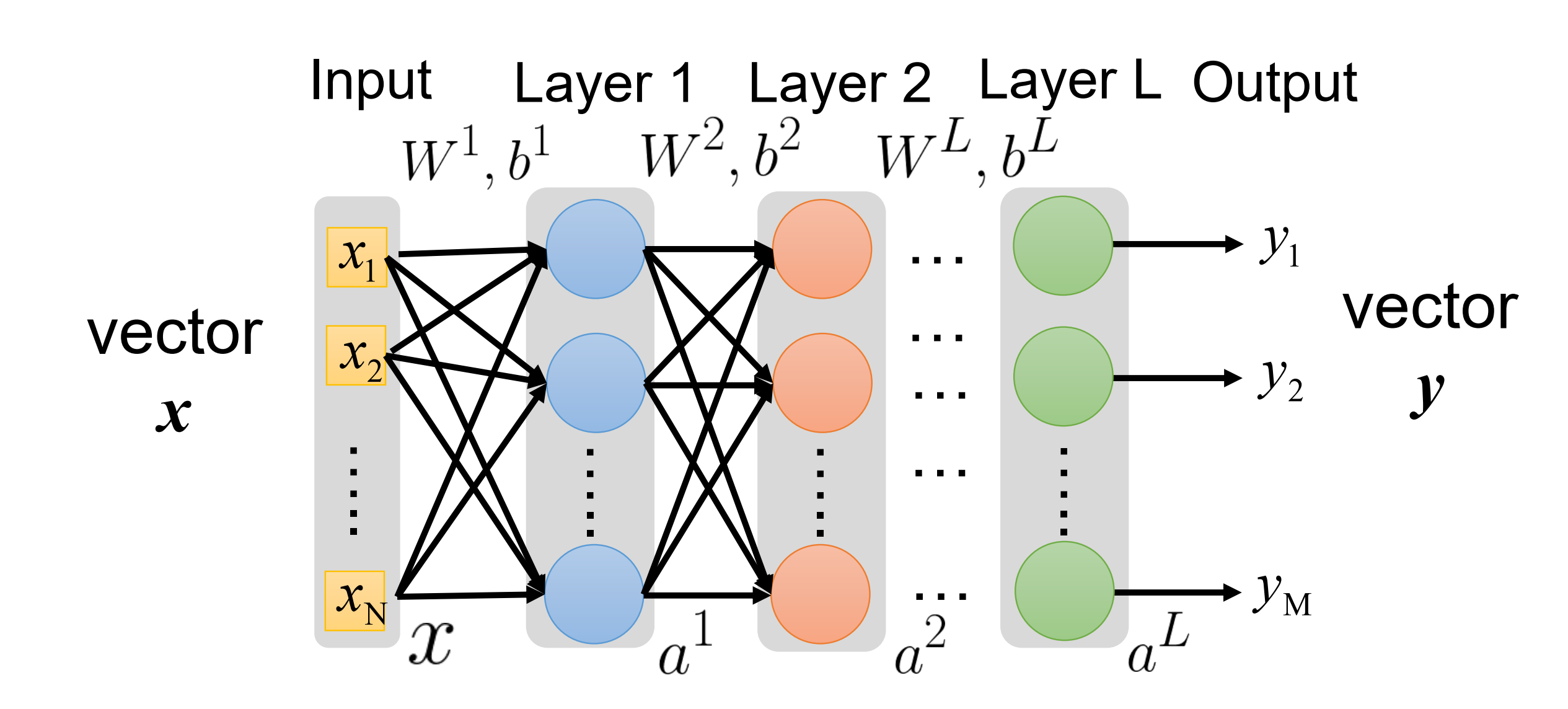
如图所示,全连接前馈神经网络,实现了
先定义一些参数:
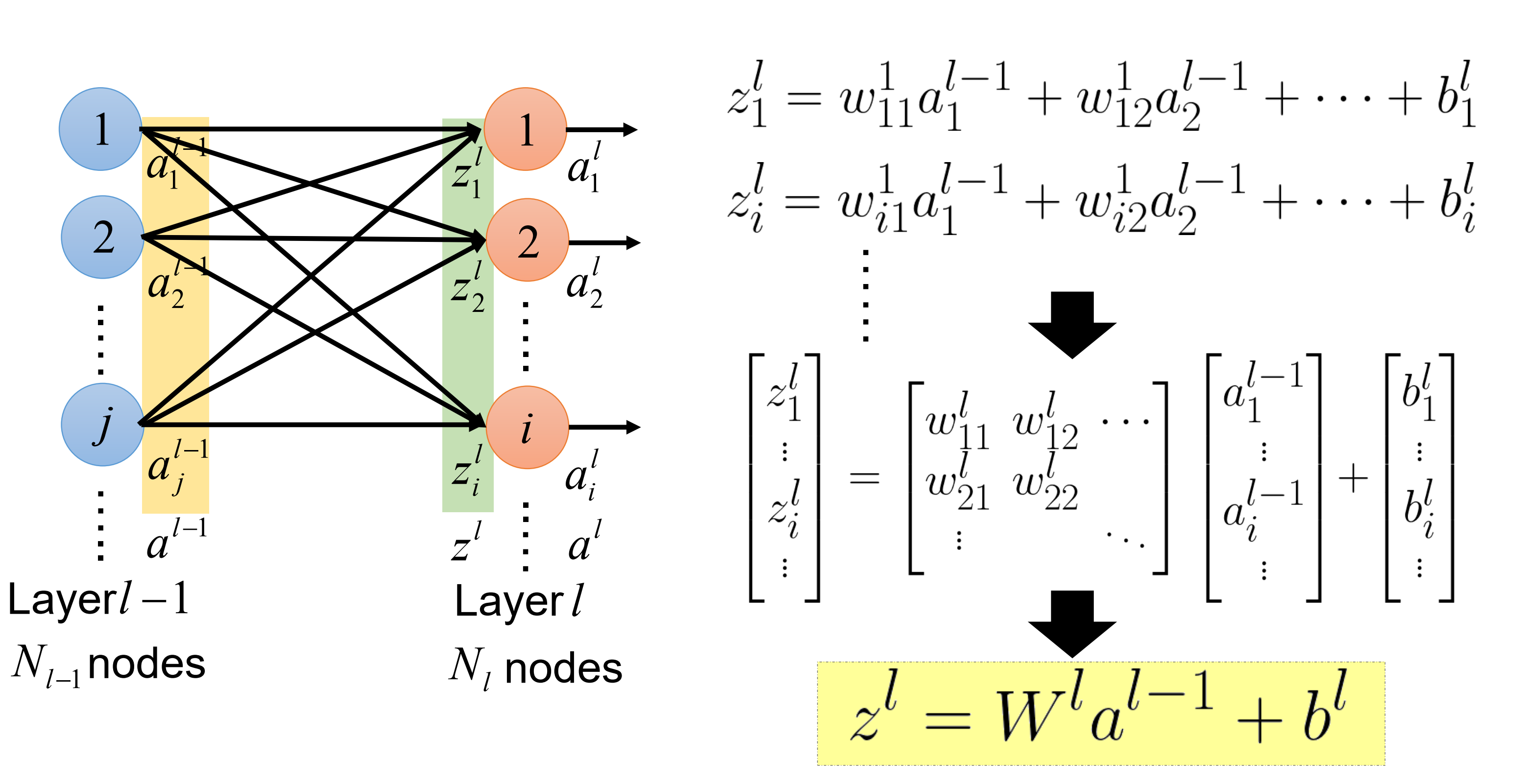
具体来说, 先看最后一层关系——从a到z,如上图。而从z到a:如下图
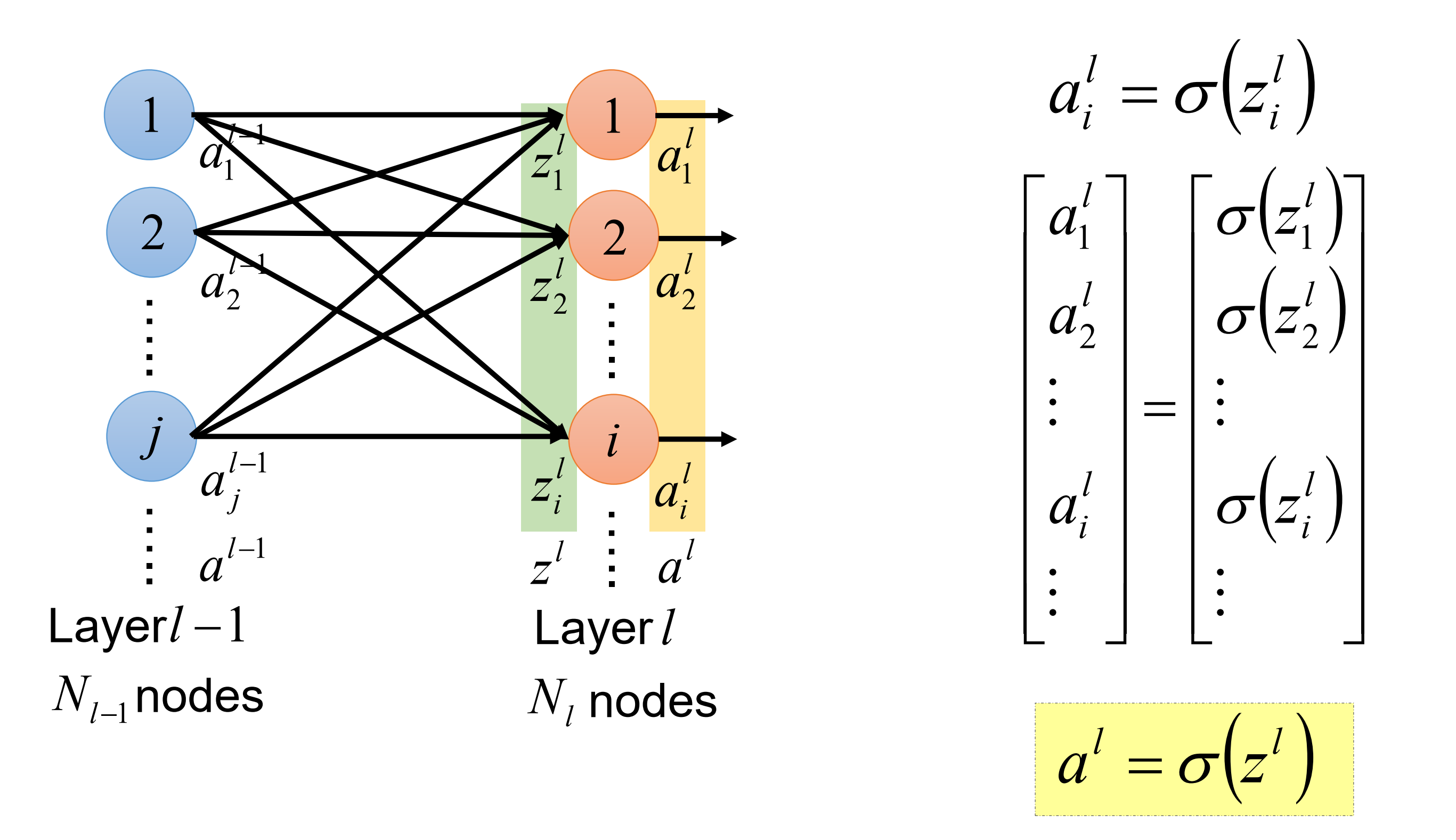
注意z到a的中间加了激活函数。这里也会产生一个梯度,$ \frac{\partial a}{ \partial z} $
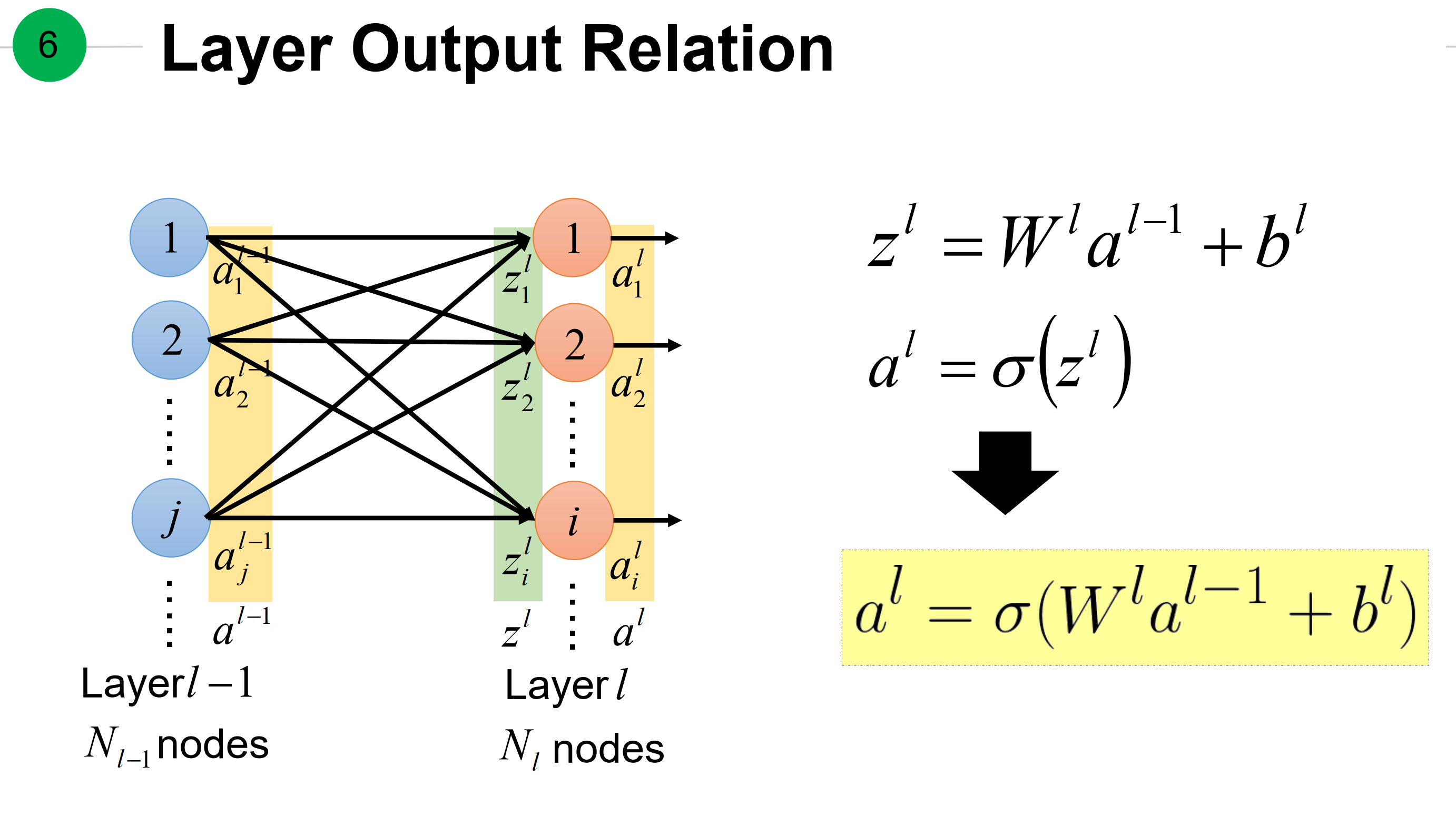
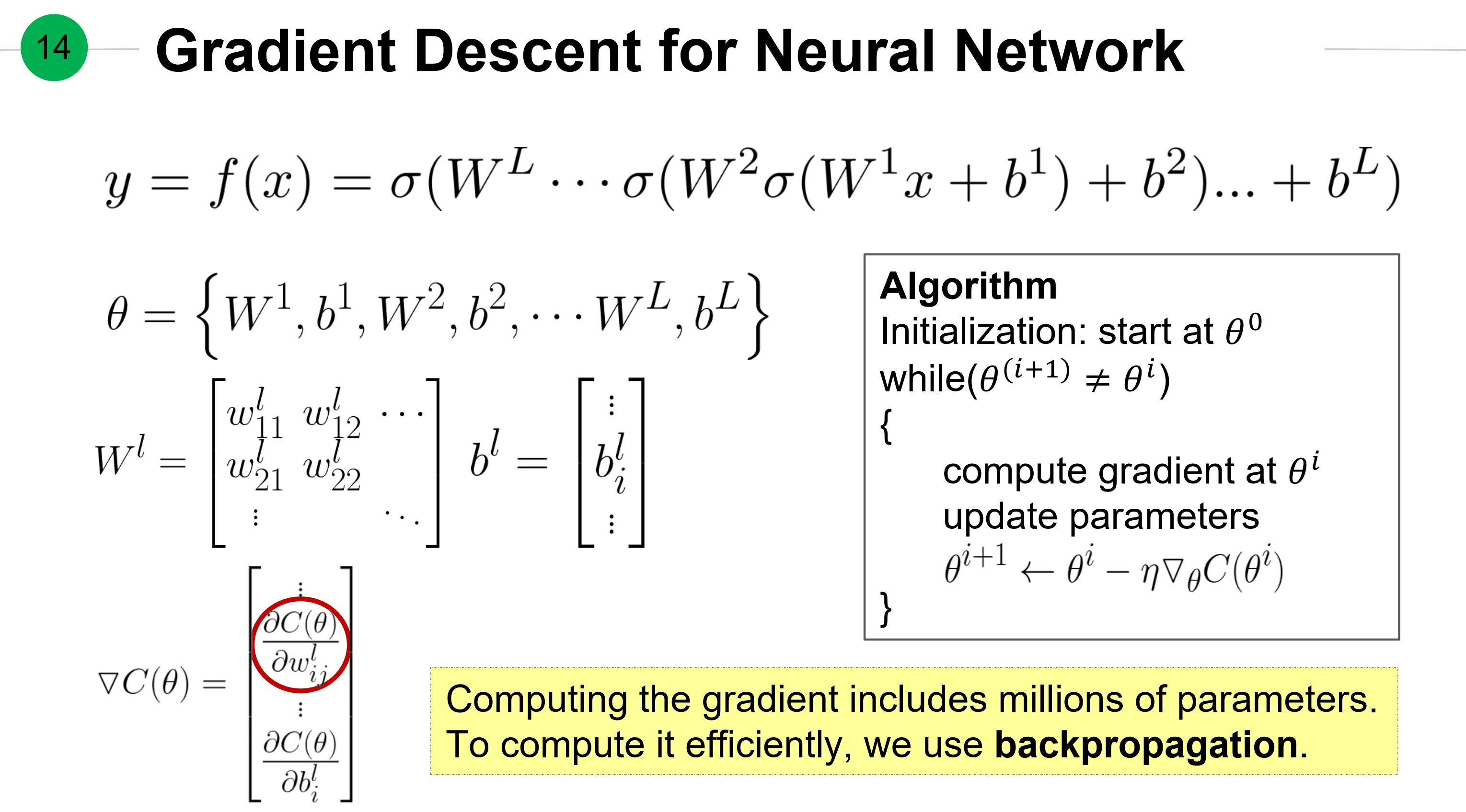
全连接神经网络的前向过程。
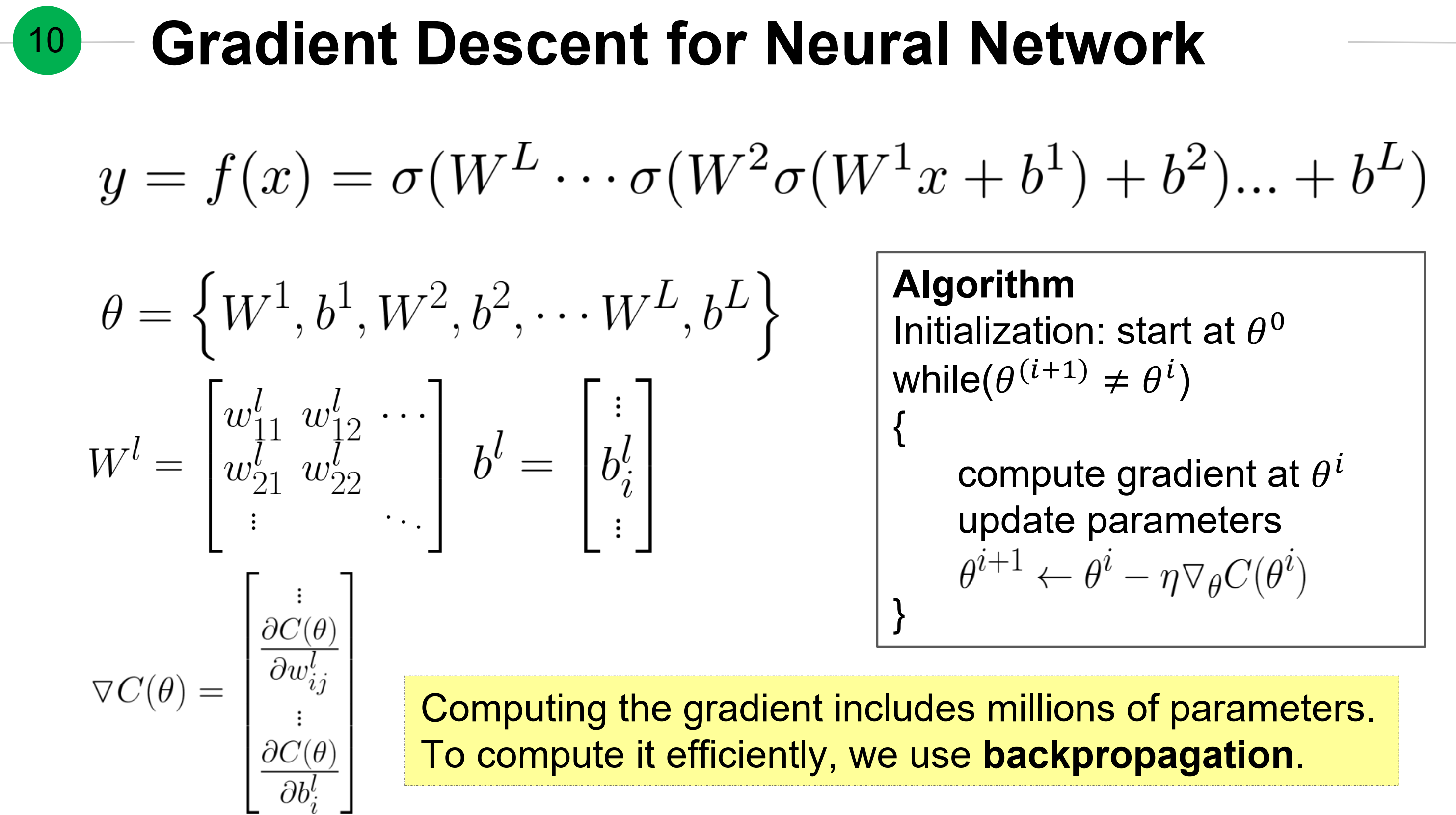
对神经网络的梯度下降算法及记号。
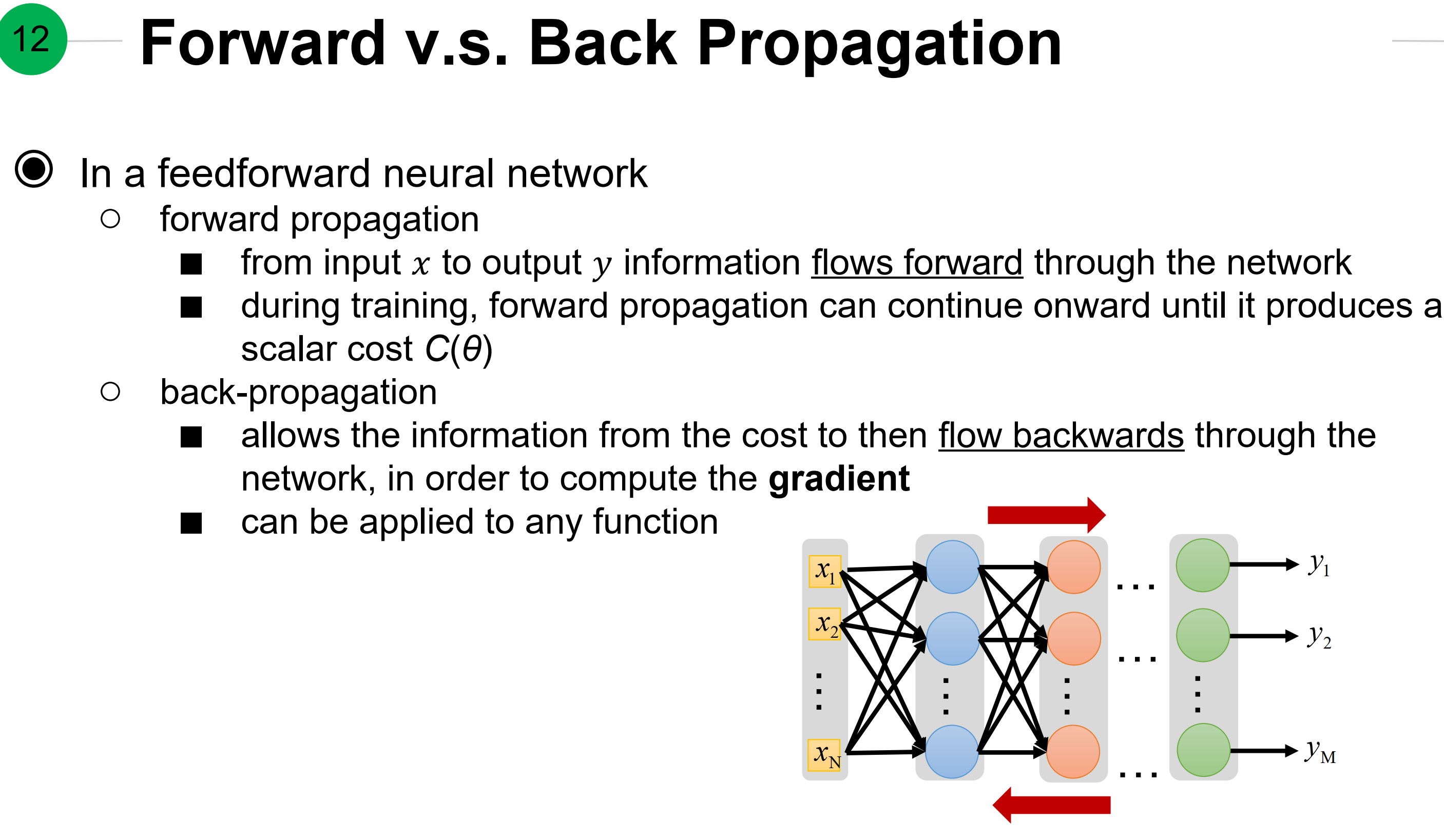
前向与后向传播比较:
- 在前馈神经网络中
- 前向
- 信息流向从输入x到输出y
- 在训练中,前向传播能持续知道产生标量$C(\theta)$
- 反向
- 允许信息从损失反向流过整个网络,放在计算完整的梯度
- 适合任何函数
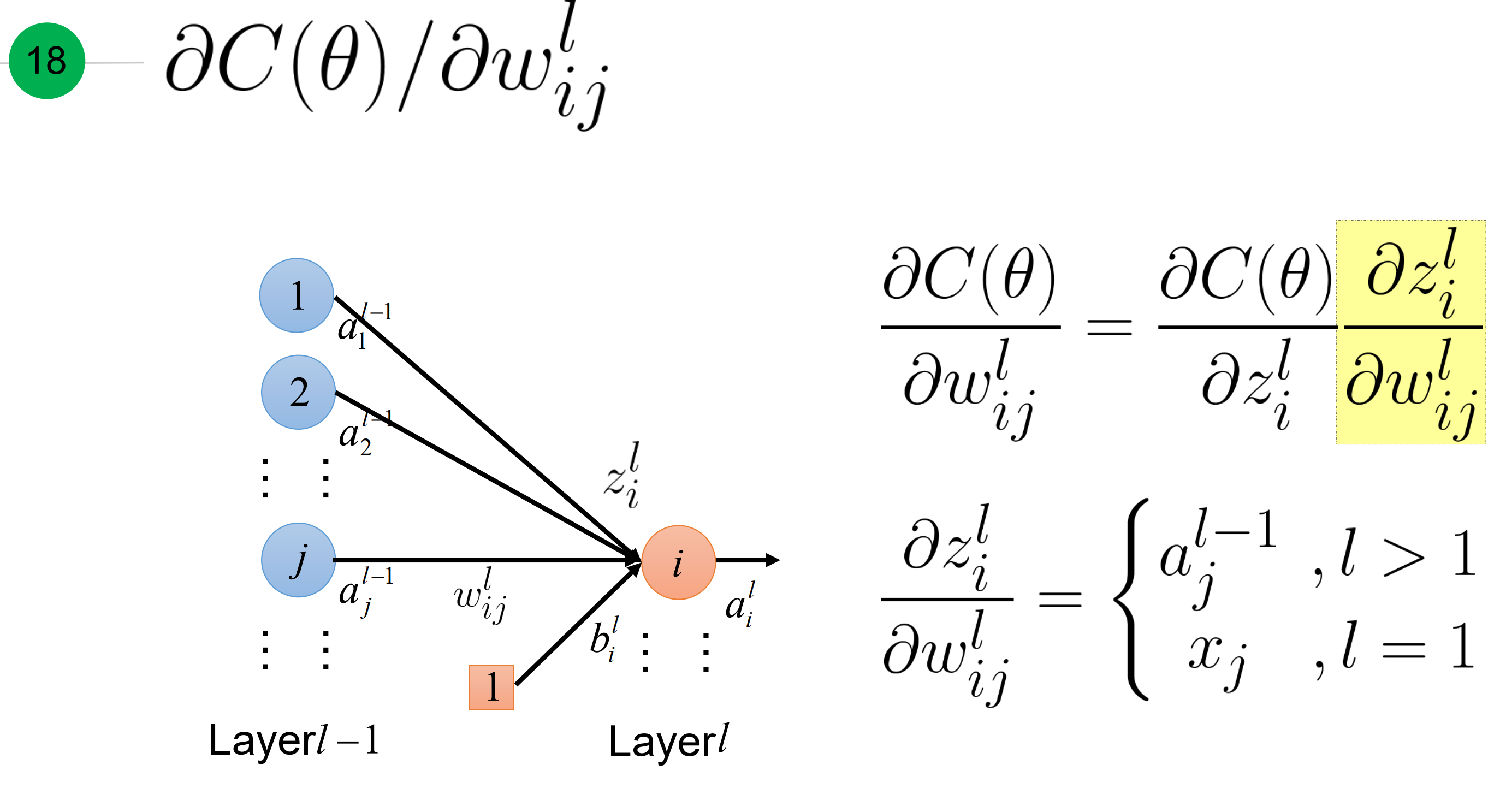
- 前向
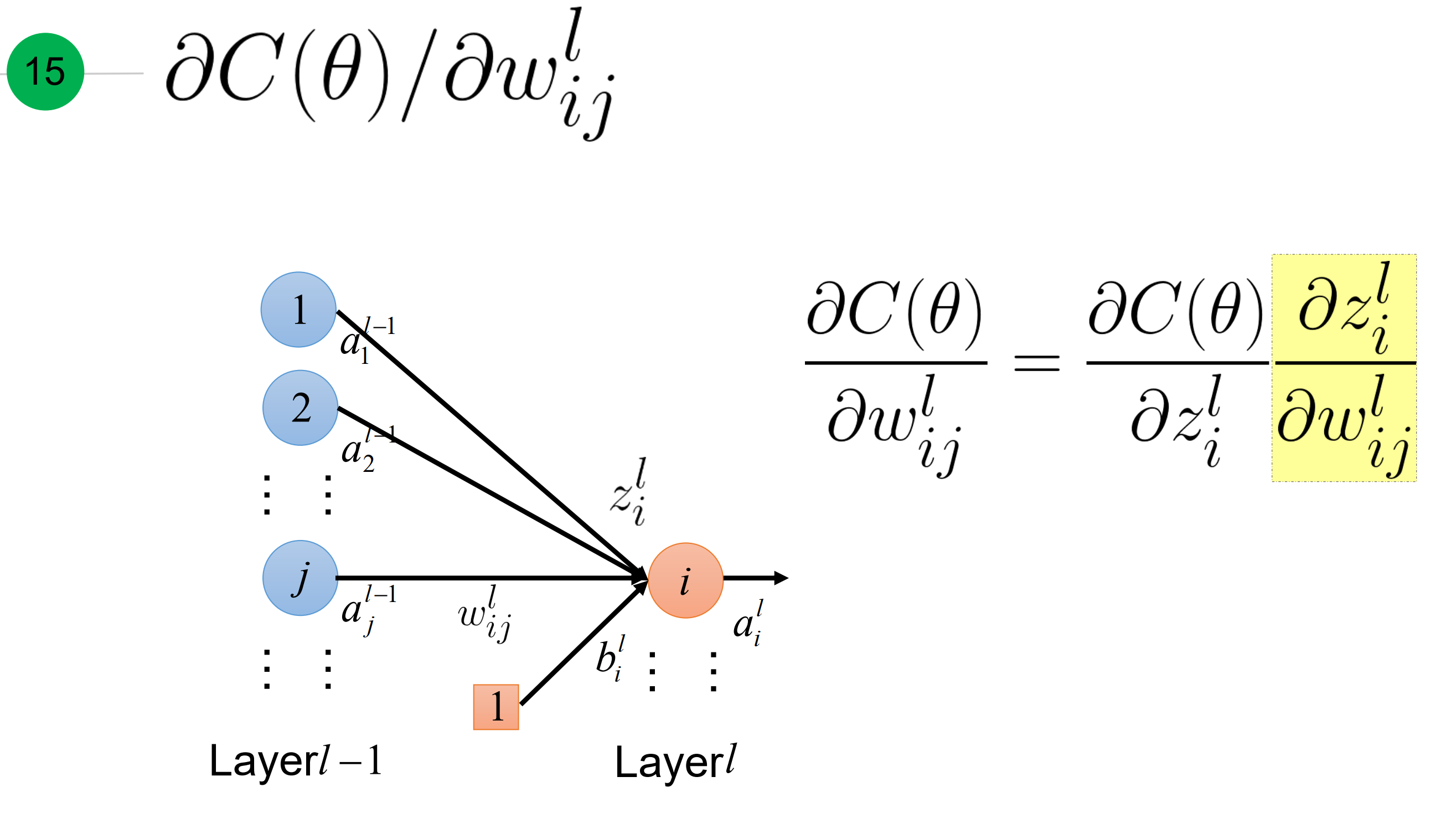
看这里,红色所示到底代表损失函数对单一权重$w^{l}_{ij}$的梯度
具体推导:
这里就等于
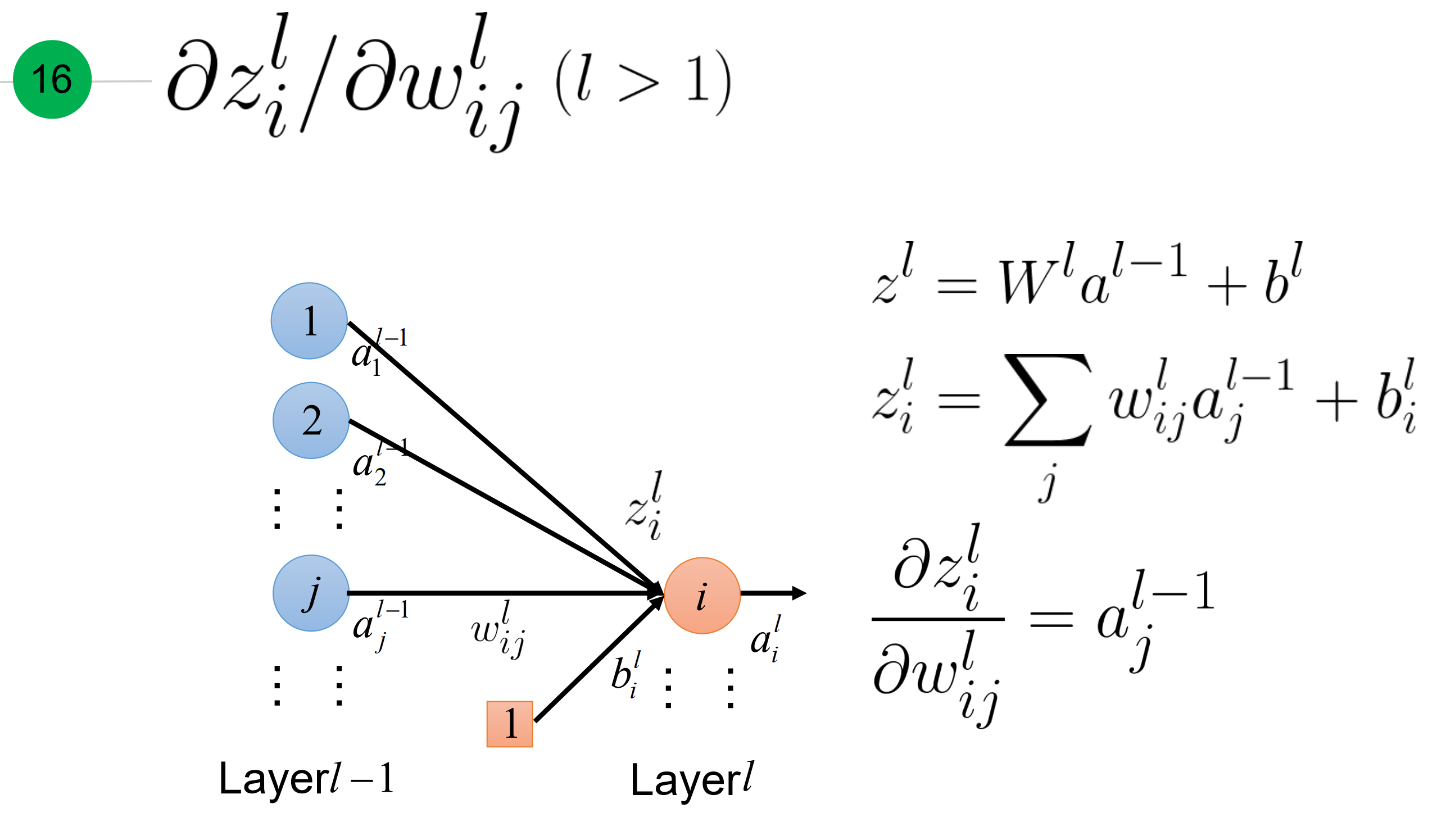
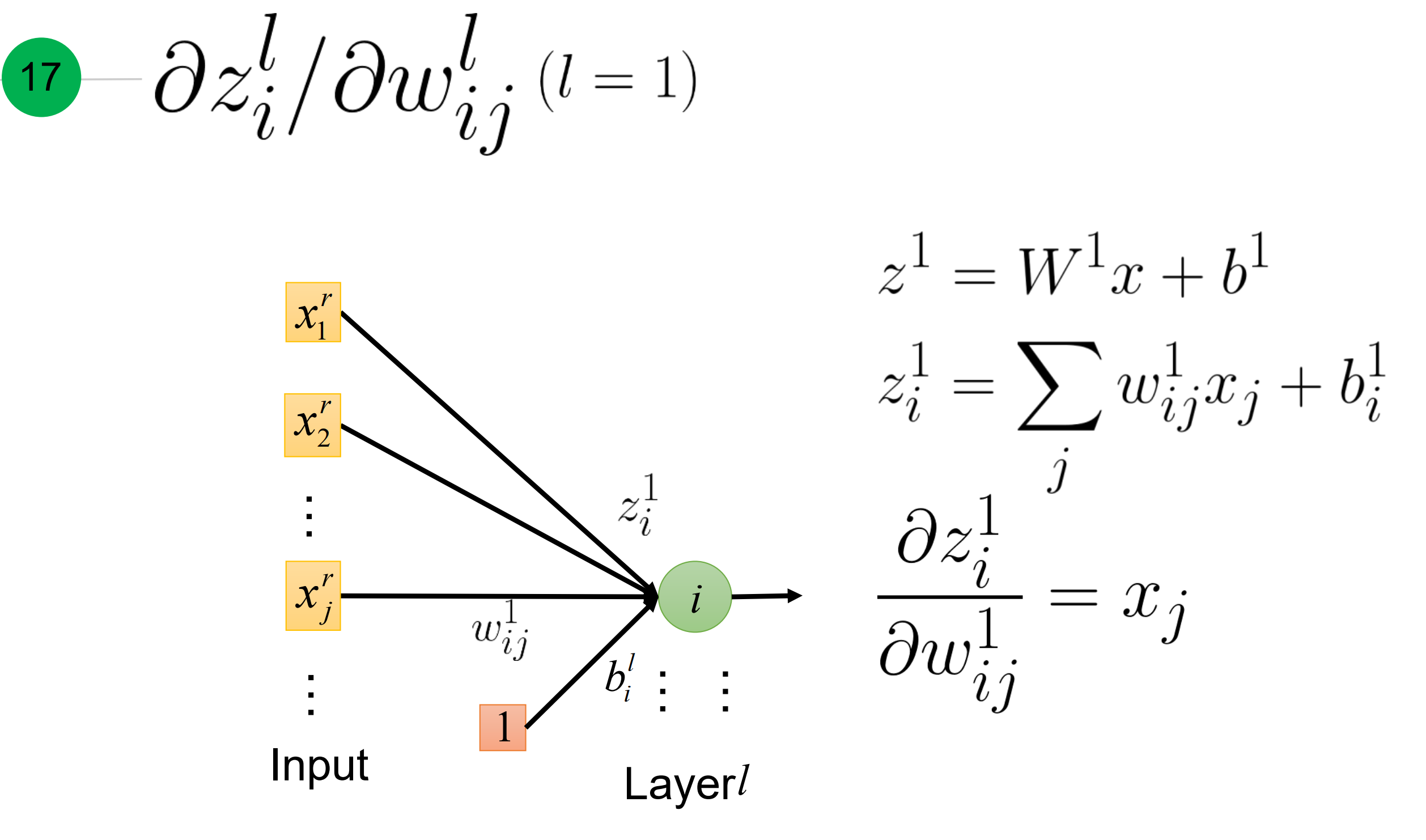
其实,就是关于$\theta$损失函数关于参数$w_{ij}^l$的梯度 可以 表达为: 损失函数对于激活函数输入z的梯度,乘以 激活函数输入z对对应权重的梯度。那后面这一项等于什么呢? 下面两张张slide解释了:
- 当层数大于1,等于对应的前一层激活函数的输出a
- 当层数为1时, 等于对应的训练的输入input x
总结一下,激活函数输出z对权重的梯度,如下。
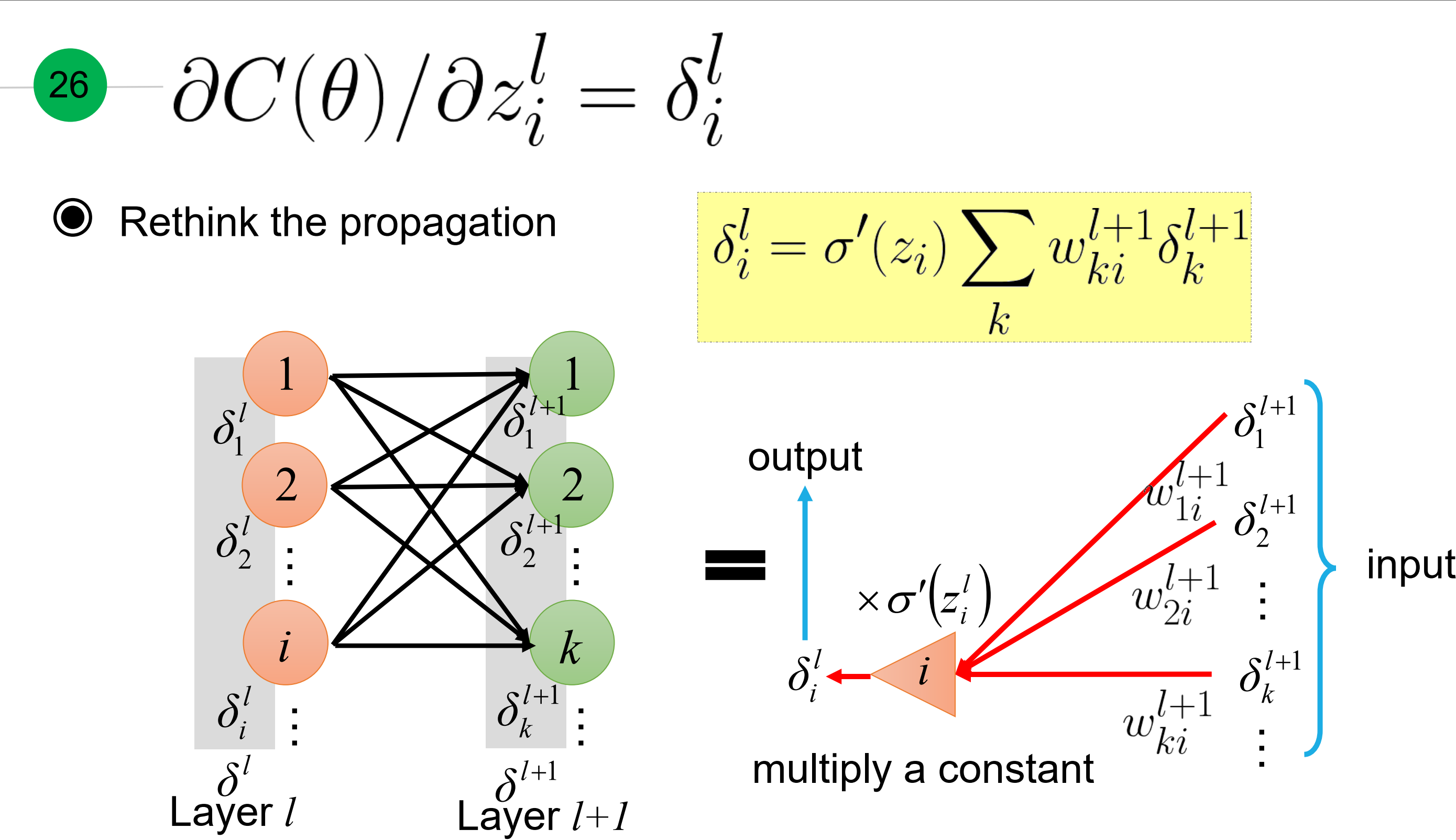
现在只要求$\frac{\partial C(\theta)}{ \partial z}$, 如下所示
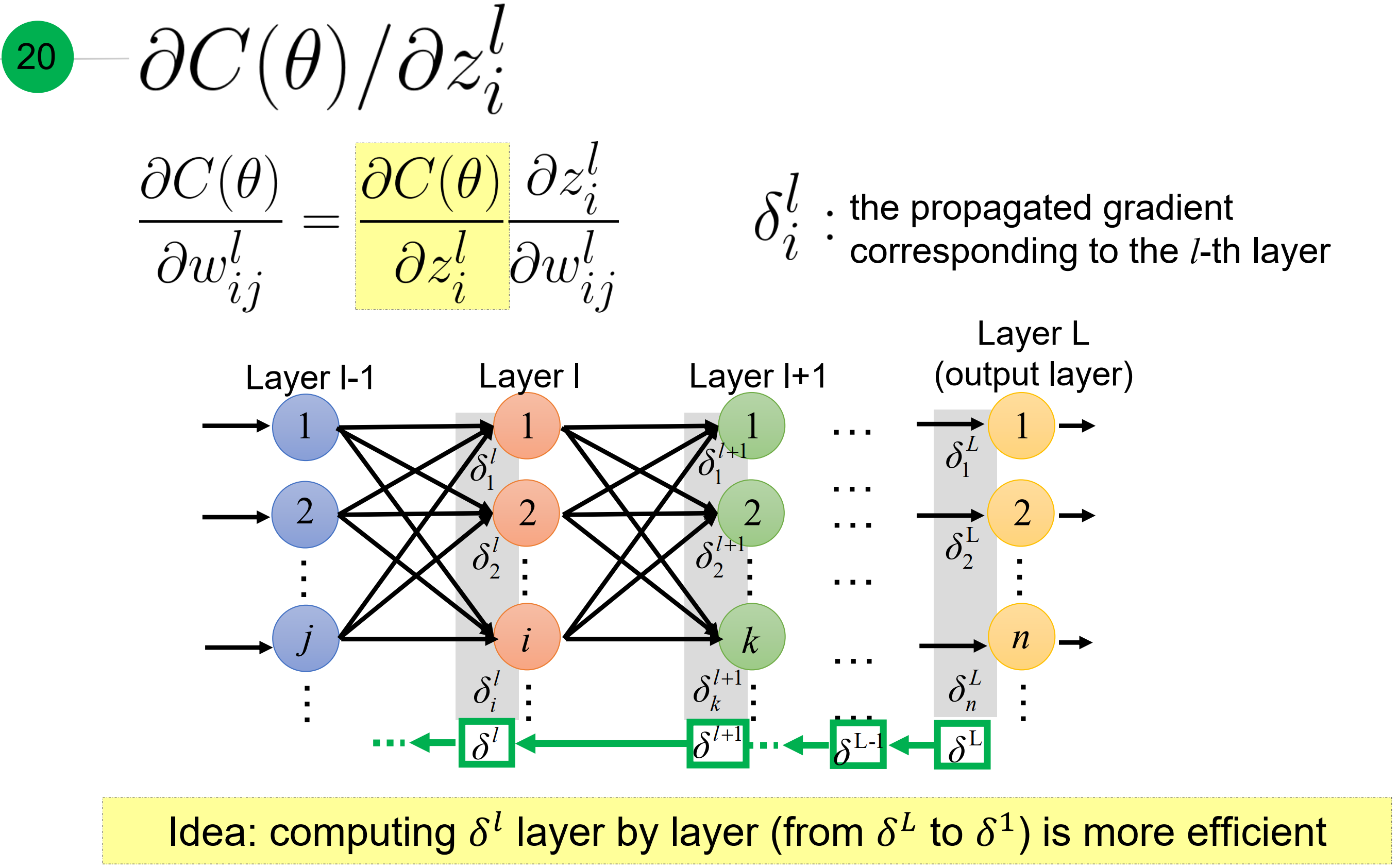
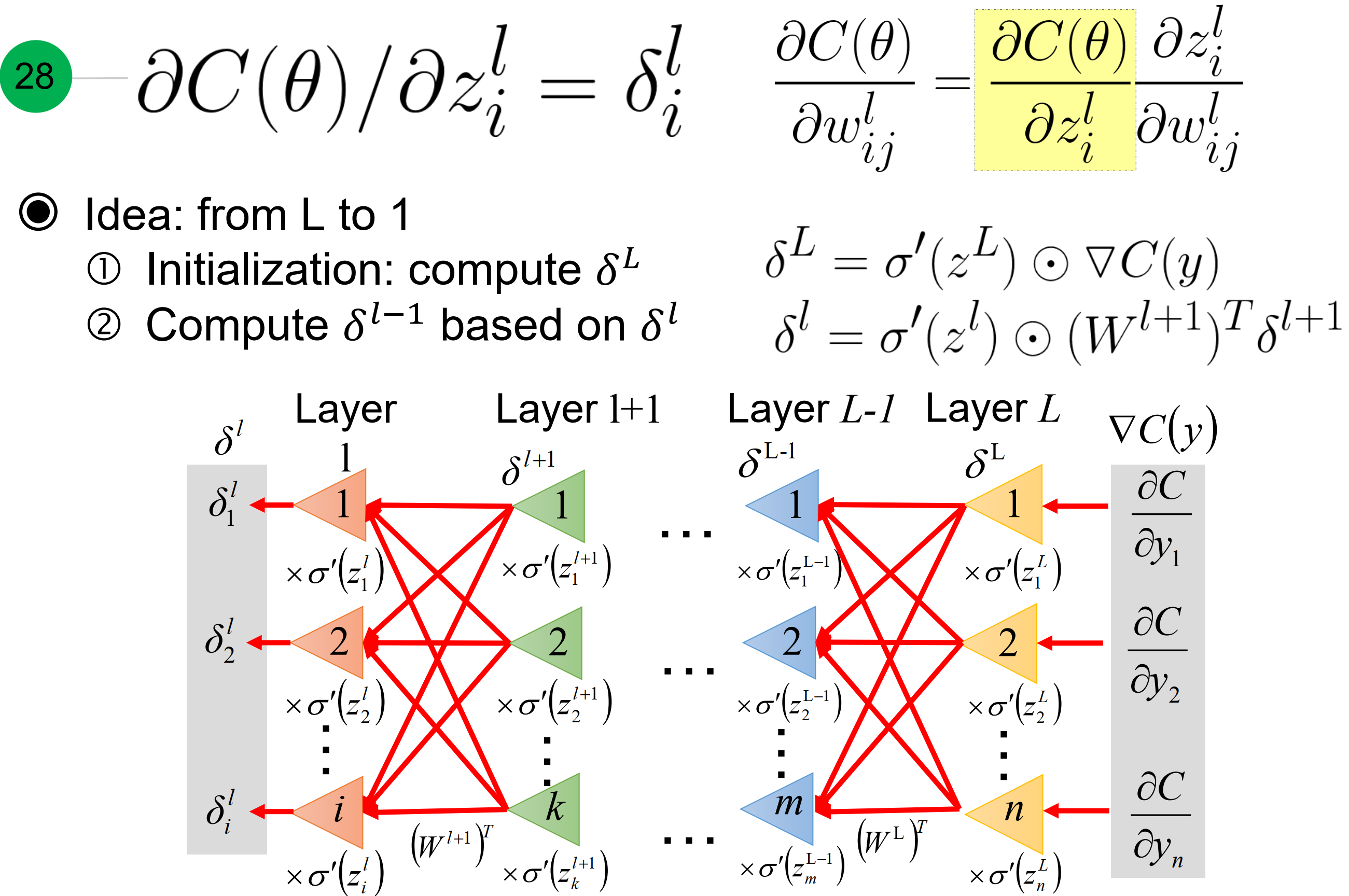
其中,引入个残差符号$\delta_i^j$, 代表第l层第i个节点的梯度。而且,利用从L层到1层的传播特性。

先计算l层的梯度,因为激活函数输入z,发生$\Delta z$的变化, 激活函数的输出就会发生$\Delta a$的变化, 就等于输出y的变化$\Delta y$,引起$\Delta C$的变化。
而$ \frac{\partial C}{ \partial y_i}$, 跟损失函数有关,比如均方差损失,交叉熵损失….

而$\frac{\partial y_i}{ \partial z_i^L}$的梯度就是激活函数在$z^L$的梯度,因此总体可以看作是激活函数在$z^L$的梯度与损失函数关于输出的梯度逐元素积。

放在整个网络中看,就是损失函数对第$l+1$层每一个z的梯度乘以每个层对$l$层a的梯度乘以第$l$层a对z的梯度。红色箭头处是$\frac{\partial C}{ \partial z_k^{l+1}}$ 等于 $\delta_k^{l+1}$, 课程上有讲k写成i了。
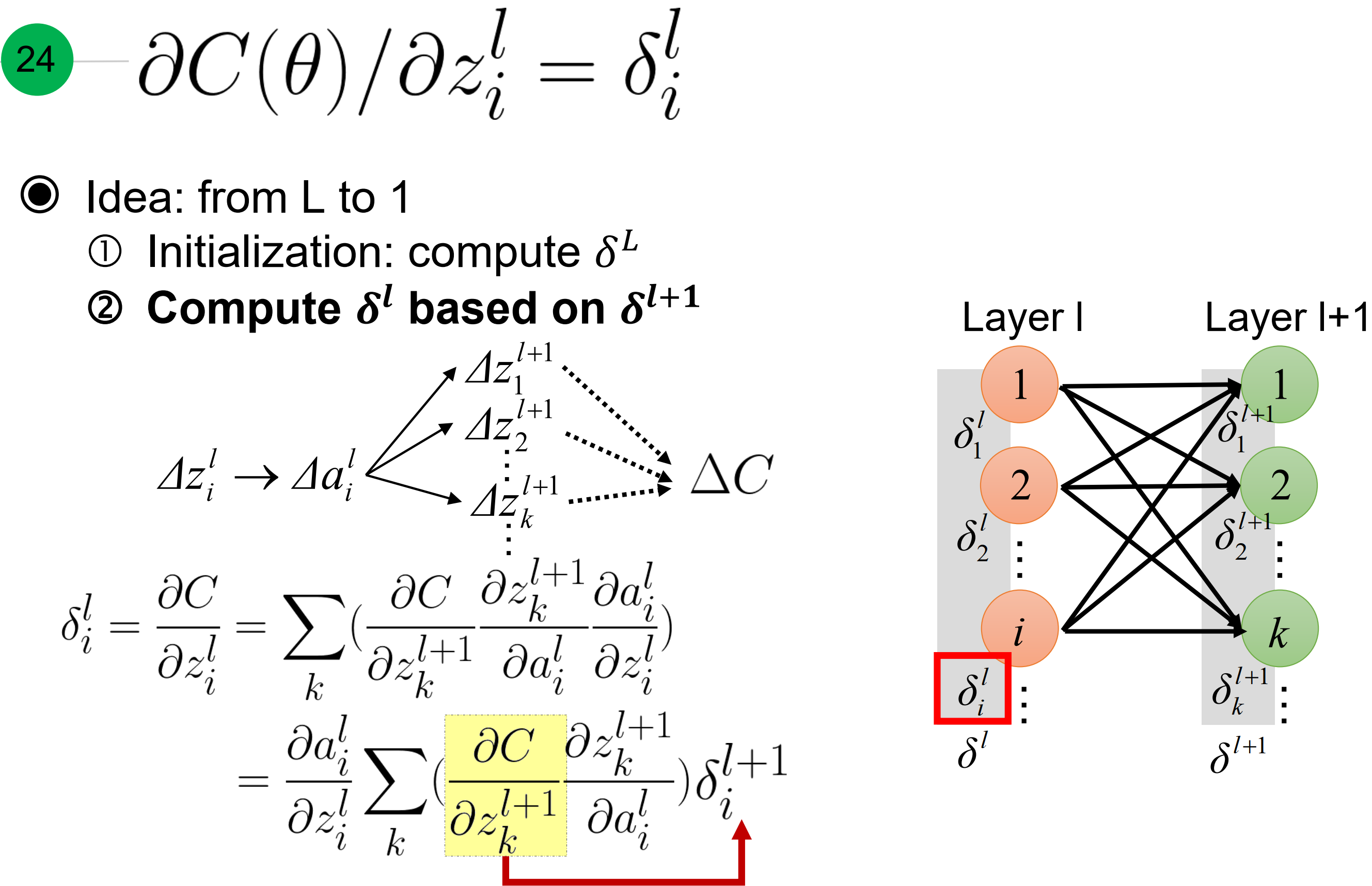
那么轻松简化成下图中.
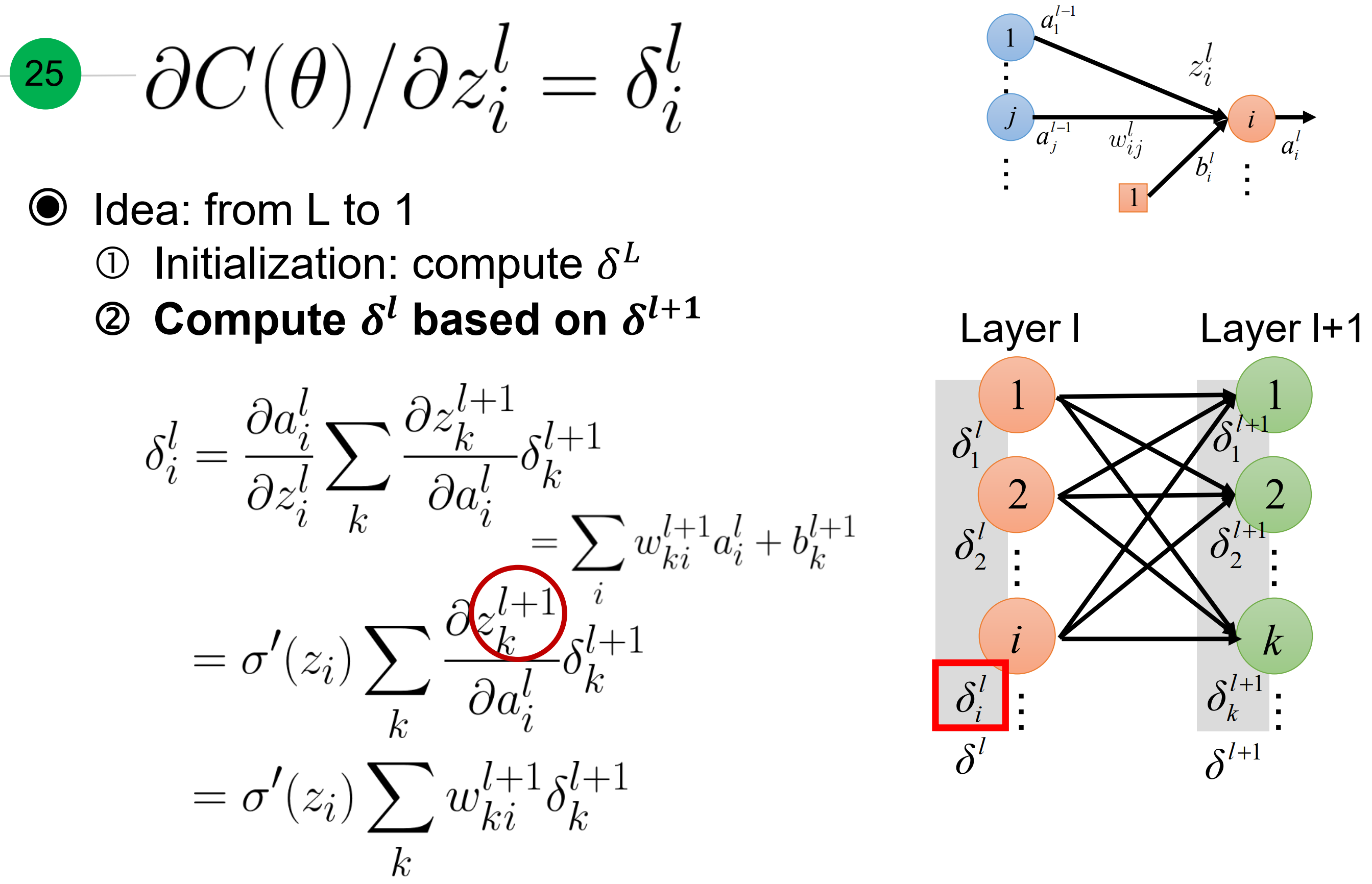
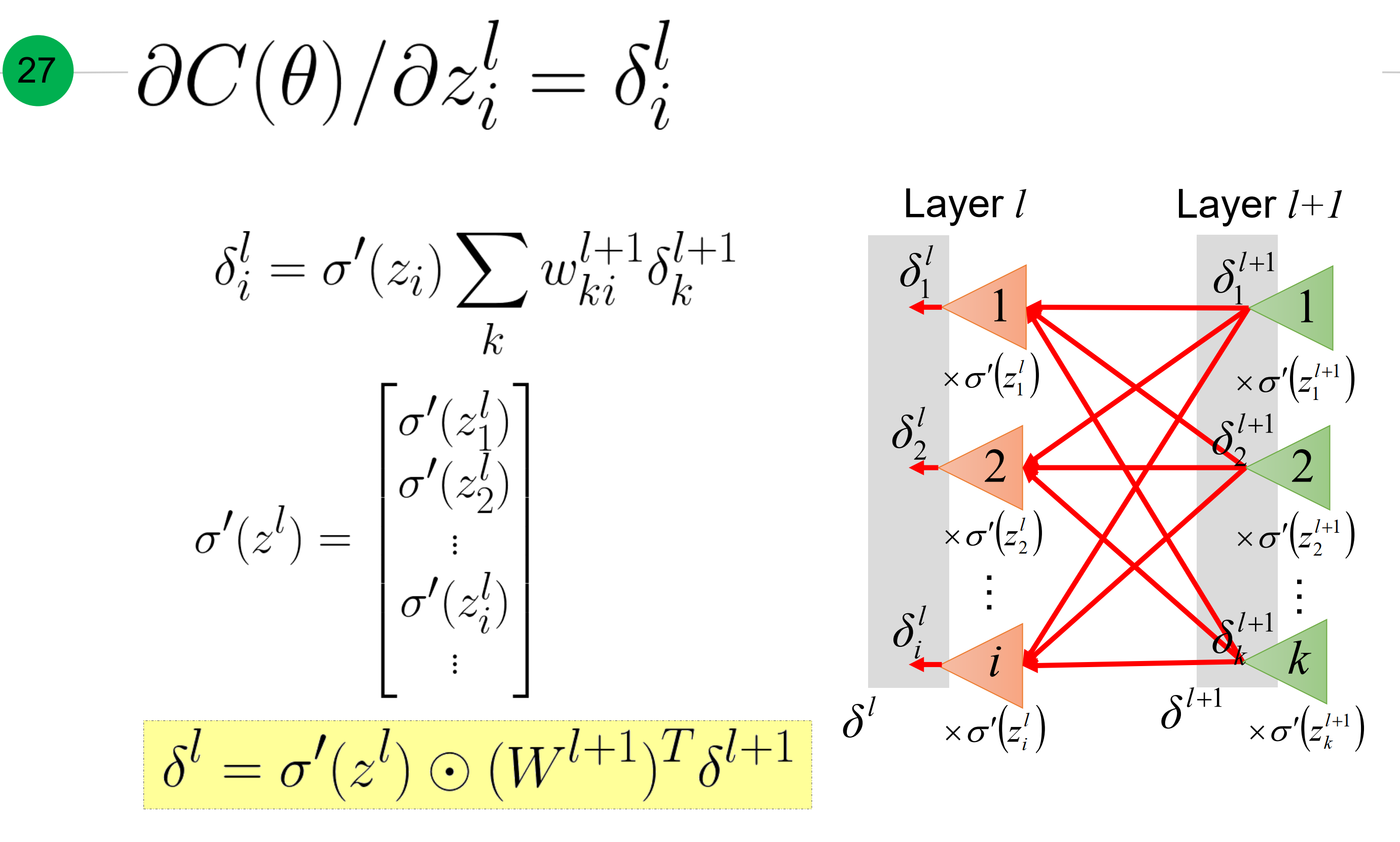
回想下梯度传播原理,就是每层梯度等于激活函数在$z_i$处梯度乘以(对应权重和下一层梯度)
写成矩阵形式就是如下
总体来看整个网络中,损失函数对权重的梯度等于损失函数对$l$层激活函数输入z的梯度,以及损失函数对权重的梯度
反向传播中,激活函数输入z对权重的梯度,分为1层网络和大于1层两种情况,分别如下

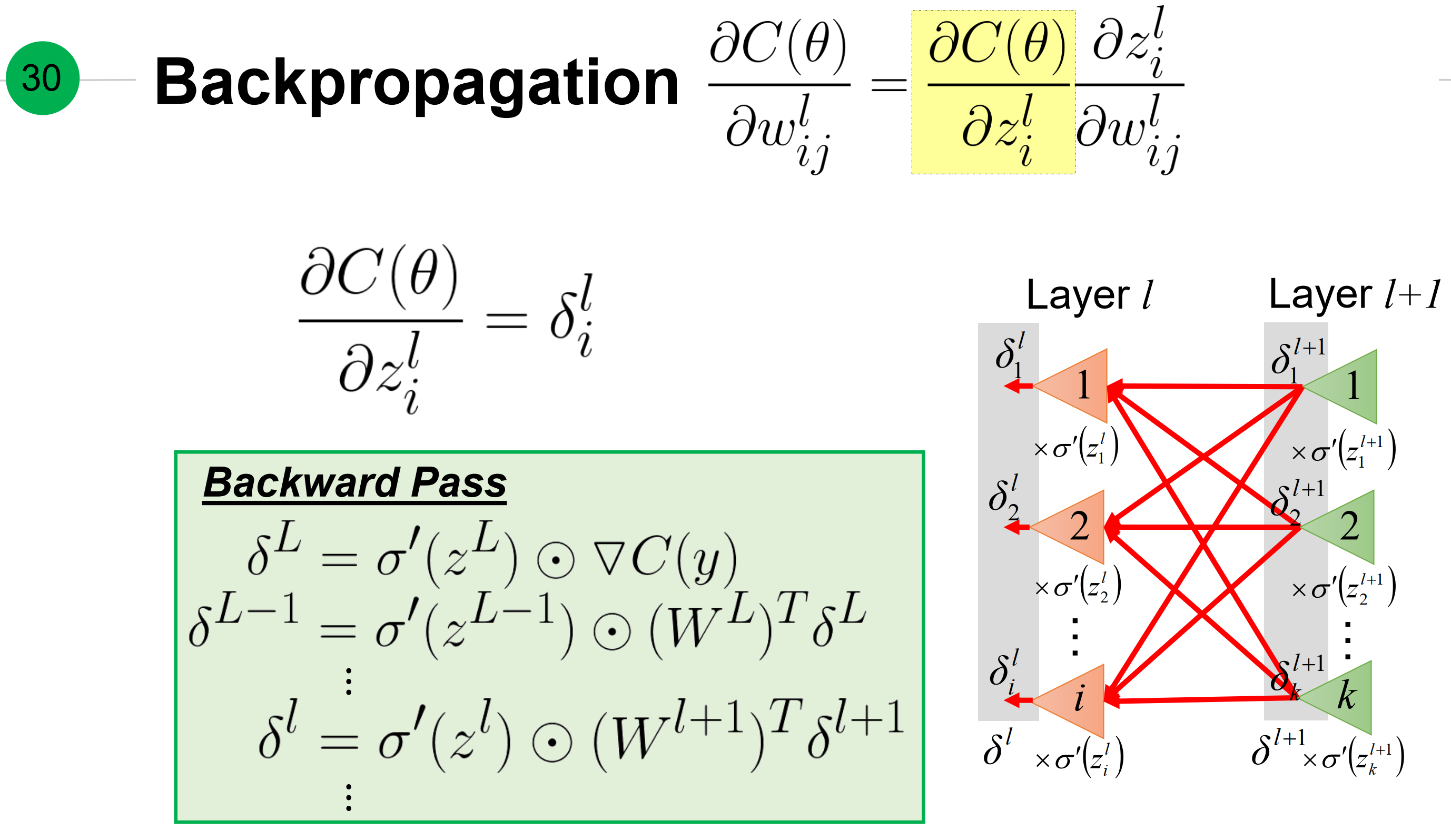
反向传播中每层激活函数处梯度,
优化中的梯度下降

总结:
计算损失函数关于权重的梯度基于从前向和反向传播中的两个提前计算量:
- 前向传播中$\delta_i^l$等于,第l层激活函数在$z^l$处梯度与 权重w和下一层$\delta$的 Hadamard积(如果是最后一层就是损失函数对z的梯度)
- 前向传播中, 激活函数输出或输入x
而这个梯度就等于上述两者相乘。(本质上是,这个神经元的输入和对应梯度的乘积,而梯度等于方向导数下降的最快方向)



